import numpy as np
import pandas as pd
import numdifftools as nd
import copy
from scipy import stats
from scipy.optimize import minimize
def AppLogDen_SL79(theta, y, X, P):
# Get parameters
[alpha, beta1, beta2, beta3, sigma2u, sigma2v,
sigma2w2, sigma2w3, sigma23] = theta[:-2]
mu = theta[-2:]
B2 = P[:, 1] - P[:, 0] + np.log(beta1) - np.log(beta2)
B3 = P[:, 2] - P[:, 0] + np.log(beta1) - np.log(beta3)
w2 = X[:, 0] - X[:, 1] - B2
w3 = X[:, 0] - X[:, 2] - B3
w = np.concatenate([w2.reshape(-1,1), w3.reshape(-1,1)], axis=1)
SigmaWW = np.array([[sigma2w3, sigma23],
[sigma23, sigma2w2]])
if np.all(np.linalg.eigvals(SigmaWW) > 0):
r = beta1 + beta2 + beta3
_lambda = np.sqrt(sigma2u/sigma2v)
sigma2 = sigma2u+sigma2v
sigma = np.sqrt(sigma2)
eps = y - alpha - X[:, 0]*beta1 - X[:, 1]*beta2 - X[:, 2]*beta3
B2 = P[:, 1] - P[:, 0] + np.log(beta1) - np.log(beta2)
B3 = P[:, 2] - P[:, 0] + np.log(beta1) - np.log(beta3)
tech_den = 2/sigma*stats.norm.pdf(eps/sigma, 0, 1)*stats.norm.cdf(-_lambda*eps/sigma, 0, 1)
logDen_Tech = np.log(tech_den)
logDen_Alloc = np.log(stats.multivariate_normal.pdf(w, mean=mu, cov=SigmaWW))
logDen = np.log(r) + logDen_Tech + logDen_Alloc
return logDen
else:
logDen = -1e10
return logDen
def AppLoglikelihood_SL79(theta, y, X, P):
logDen = AppLogDen_SL79(theta, y, X, P)
logL = -np.sum(logDen)
return logL
def AppEstimate_SL79(y, X, P):
# Starting values
alpha = -2
beta1 = 0.5
beta2 = 0.15
beta3 = 0.2;
sigma2u = 0.01
sigma2v = 0.002
sigma2w2 = 0.01
sigma2w3 = 0.01
sigma23 = 0
mu2 = 0.3
mu3 = 0.3
mu = [mu2, mu3]
theta0 = [alpha, beta1, beta2, beta3, sigma2u, sigma2v, sigma2w2, sigma2w3,
np.log((1+sigma23)/(1-sigma23))]+ mu
# Bounds to ensure sigma are positive
bounds = [(None, None) for x in range(4)] + [(1e-6, np.inf) for i in range(4)] + [(None, None) for x in range(3)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(
fun=AppLoglikelihood_SL79,
x0=theta0,
bounds=bounds,
method="L-BFGS-B",
tol = 1e-6,
options={"ftol": 1e-6, "maxiter": 1000, "maxfun": 6*1000, "maxcor": 500},
args=(y.values, X.values, P.values),
)
theta = MLE_results.x # Estimated parameter vector
logMLE = MLE_results.fun * -1 # Log-likelihood at the solution
# standard errors
# gradient calculation
delta = 1e-6
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = np.copy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_SL79(theta1, y.values, X.values, P.values) - AppLogDen_SL79(theta, y.values, X.values, P.values))/delta
# Hessian calculation
hessian = nd.Hessian(f=AppLoglikelihood_SL79, method="central", step=1e-5)(theta, y.values, X.values, P.values)
OPG = grad.T@grad
ster = np.sqrt(np.diag(np.linalg.inv(OPG)))
ster_rob = np.sqrt(np.diag(np.linalg.inv(-hessian)@OPG@np.linalg.inv(-hessian)))
return theta, ster, ster_rob, logMLE
def MatrixToCholeski(Sigma):
SigmaChol = np.linalg.cholesky(Sigma)
CholOfSigma = SigmaChol[np.tril_indices(SigmaChol.shape[0], k=0)] # elements of lower triangle of the choleski
return CholOfSigma
def CholeskiToMatrix(CholOfSigma):
SigmaChol = np.zeros((3,3))
SigmaChol[np.tril_indices(SigmaChol.shape[0], k=0)] = CholOfSigma
Sigma = SigmaChol@SigmaChol.T
return Sigma
def AppLogDen_SL80(theta, y, X, P):
# Get parameters
[alpha, beta1, beta2, beta3] = theta[:4]
sigma2v = theta[-3]
mu = np.concatenate([np.array([0]), theta[-2:]])
#Sigma = CholeskiToMatrix(theta[4:10])
Sigma = np.zeros((3,3))
Sigma[np.tril_indices(Sigma.shape[0], k=0)] = theta[4:10]
Sigma = Sigma + Sigma.T-np.diag(np.diag(Sigma))
G = np.array(Sigma)
G[0, 0] = G[0, 0] + sigma2v
Gstar = np.array(G)
Gstar[0, 1:3] = -G[0, 1:3]
Gstar[1:3, 0] = -G[1:3, 0]
eps = y - alpha - X[:,0] * beta1 - X[:,1] * beta2 - X[:,2] * beta3
B2 = P[:,1] - P[:,0] + np.log(beta1) - np.log(beta2)
B3 = P[:,2] - P[:,0] + np.log(beta1) - np.log(beta3)
w2 = X[:,0] - X[:,1] - B2
w3 = X[:,0] - X[:,2] - B3
w = np.array([w2, w3]).T
all_values = np.array([eps, w2, w3]).T
r = beta1 + beta2 + beta3
InvSigma = np.linalg.inv(Sigma)
A = (eps + sigma2v * w@InvSigma[0, 1:3]) / np.sqrt(sigma2v) * np.sqrt(np.linalg.det(Sigma) / np.linalg.det(G))
Astar = (eps - sigma2v * w@InvSigma[0, 1:3]) / np.sqrt(sigma2v) * np.sqrt(np.linalg.det(Sigma) / np.linalg.det(G))
term1 = stats.multivariate_normal.pdf(all_values, mean=mu, cov=G)
term2 = stats.multivariate_normal.pdf(all_values, mean=mu, cov=Gstar)
logDen = np.log(r) + np.log(stats.norm.cdf(-A, 0, 1) * term1 + stats.norm.cdf(-Astar, 0, 1) * term2)
return logDen
def AppLoglikelihood_SL80(theta, y, X, P):
theta = transform_parameters(theta=theta)
logDen = AppLogDen_SL80(theta, y, X, P)
logL = -np.sum(logDen)
return logL
def transform_parameters(theta):
transformed_theta = copy.deepcopy(theta)
Sigma = CholeskiToMatrix(theta[4:10])
transformed_theta[4:10] = Sigma[np.tril_indices(Sigma.shape[0], k=0)]
return transformed_theta
def AppEstimate_SL80(y, X, P):
# Starting values
alpha = -2.6
beta1 = 0.5
beta2 = 0.2
beta3 = 0.2;
sigma2u = 0.14
sigma2v = 0.1
sigmau2 = 0
sigmau3 = 0
sigma22 = 0.2
sigma33 = 0.2
sigma23 = 0.1
mu2 = 0.5
mu3 = 0.1
mu = [mu2, mu3]
Sigma = np.array([[sigma2u, sigmau2, sigmau3],
[sigmau2, sigma22, sigma23],
[sigmau3, sigma23, sigma33]])
CholOfSigma = MatrixToCholeski(Sigma) # 1x6 vector of lower triangle of chol of Sigma
theta0 = np.array([alpha, beta1, beta2, beta3] + CholOfSigma.tolist() + [sigma2v] + mu)
# Bounds to ensure sigma are positive
bounds = [(None, None) for x in range(4 + len(CholOfSigma))] + [(1e-6, np.inf) for i in range(3)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(
fun=AppLoglikelihood_SL80,
x0=theta0,
bounds=bounds,
method="Nelder-Mead",
tol = 1e-6,
options={"maxiter": 20000},
args=(y.values, X.values, P.values),
)
# transform parameters
theta_ = MLE_results.x
theta = transform_parameters(theta=theta_)
logMLE = MLE_results.fun * -1 # Log-likelihood at the solution
# standard errors
# gradient calculation
delta = 1e-6
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = np.copy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_SL80(theta1, y.values, X.values, P.values) - AppLogDen_SL80(theta, y.values, X.values, P.values))/delta
# Hessian calculation
hessian = nd.Hessian(f=AppLoglikelihood_SL80, method="central", step=1e-6)(theta_, y.values, X.values, P.values)
# Hessian transformation
D = np.eye(len(theta_))
for i in range(len(theta_)):
theta1 = copy.deepcopy(theta_)
theta1[i] = theta_[i] + delta
D[:,i] = (transform_parameters(theta1)-transform_parameters(theta_))/delta
OPG = grad.T@grad
ster = np.sqrt(np.diag(np.linalg.inv(OPG)))
ster_rob = np.sqrt(np.diag(D.T@np.linalg.inv(hessian)@D@OPG@D.T@np.linalg.inv(hessian)@D))
return theta, ster, ster_rob, logMLE6 Chapter 6: Modelling Dependence in Production Systems
6.1 Exercise 6.1: The SL79 and SL80 estimators for US utilities.
This exercise implements the SL79 and SL80 estimators for the U.S. utilities dataset steamelectric.xls. The data for this exercise is the same as the data used by Rungsuriyawiboon and Stefanou (2007) and Amsler et al. (2021). The output variable is net power generated, in megawatt-hours; the inputs are fuel, labor and maintenance (L&M), and capital; the input prices are (i) the average fuel price in dollars per BTU, (ii) cost-share weighted price of labor and maintenance, where the price of labor is company-wide average wage rate and the price of maintenance is a price index of electrical supplies from the Bureau of Labor Statistics, and (iii) the yield of the latest debt issued by the firm. Quantities of fuel, L&M and capital are computed by dividing the reported fuel expenses, aggregate L&M costs and capital costs by the relevant prices. The dataset contained 1008 observations but upon data cleaning as described by Amsler et al. (2021) we ended up with 934 observations. All of the parameters are as defined earlier; in addition, \(\mu_{j}\)’s are the means of the allocative inefficiencies \(\omega_{j}\)’s which are permitted to be non-zero. We report both the “OPG” and robust “sandwich” versions (Rob) of the standard errors (see Appendix 4.B).
# import data
data = pd.read_excel('steamelectric.xlsx')
data['fuel_price_index'] = np.nan
data.iloc[:-1, -1] = data.iloc[:-1, 2].values/data.iloc[1:,2].values
data['LM_price_index'] = np.nan
data.iloc[:-1, -1] = data.iloc[:-1, 3].values/data.iloc[1:,3].values
data.iloc[13:1007:14, :] = np.nan #drop last fuel price index for each plant
data = data.dropna()
X1 = (data['Fuel Costs ($1000)']/data['fuel_price_index'])*1000*1e-6; #fuel costs over price index
X2 = data['Operating Costs ($1000)']/data['LM_price_index']*1000*1e-6; #LM costs over price index
X3 = data['Capital ($1000)']/1000; # capital
X = np.log(pd.concat([X1, X2, X3], axis=1))
P = np.log(data[['fuel_price_index', 'LM_price_index', 'User Cost of Capital']])
y = np.log(data['Output (MWhr)']*1e-6) # output ml MWpH
(SL79_theta, SL79_sterr, SL79_ster_rob, SL79_logMLE) = AppEstimate_SL79(y=y,
X=X,
P=P)
(SL80_theta, SL80_sterr, SL80_ster_rob, SL80_logMLE) = AppEstimate_SL80(y=y,
X=X,
P=P)
# Display the results as a table
results = pd.DataFrame(
columns=["SL79 Est", "SL79 St.Er.(OPG)", "SL79 St.Er.(Rob)",
"SL80 Est", "SL80 St.Er.(OPG)", "SL80 St.Er.(Rob)"],
index=[
r"$$\alpha$$",
r"$$\beta_{1}$$",
r"$$\beta_{2}$$",
r"$$\beta_{3}$$",
r"$$\sigma_{u}^{2}$$",
r"$$\Sigma^{2u}$$",
r"$$\Sigma^{3u}$$",
r"$$\Sigma^{22}$$",
r"$$\Sigma^{23}$$",
r"$$\Sigma^{33}$$",
r"$$\sigma^{2}_{v}$$",
r"$$\mu_{2}$$",
r"$$\mu_{3}$$",
],
)
SL79_theta = np.round(SL79_theta.reshape(-1, 1), 3)
SL79_sterr = np.round(SL79_sterr.reshape(-1, 1), 3)
SL79_ster_rob = np.round(SL79_ster_rob.reshape(-1, 1), 3)
SL80_theta = np.round(SL80_theta.reshape(-1, 1), 3)
SL80_sterr = np.round(SL80_sterr.reshape(-1, 1), 3)
SL80_ster_rob = np.round(SL80_ster_rob.reshape(-1, 1), 3)
SL79_frontier = np.concatenate(
[
SL79_theta[:4],
SL79_sterr[:4],
SL79_ster_rob[:4]
],
axis=1,
)
SL80_frontier = np.concatenate(
[
SL80_theta[:4],
SL80_sterr[:4],
SL80_ster_rob[:4]
],
axis=1,
)
SL79_sigmas = np.concatenate(
[
np.concatenate([SL79_theta[[4]], np.array([[np.nan, np.nan]]).T, SL79_theta[[6]], SL79_theta[[8]], SL79_theta[[5]], SL79_theta[[9]]], axis=0),
np.concatenate([SL79_sterr[[4]], np.array([[np.nan, np.nan]]).T, SL79_sterr[[6]], SL79_sterr[[8]], SL79_sterr[[5]], SL79_sterr[[9]]], axis=0),
np.concatenate([SL79_ster_rob[[4]], np.array([[np.nan, np.nan]]).T, SL79_ster_rob[[6]], SL79_ster_rob[[8]], SL79_ster_rob[[5]], SL79_ster_rob[[9]]], axis=0),
],
axis=1,
)
SL80_sigmas = np.concatenate(
[
np.concatenate([SL80_theta[4:6], np.array([SL80_theta[7], SL80_theta[6]]), SL80_theta[8:-2]], axis=0),
np.concatenate([SL80_sterr[4:6], np.array([SL80_sterr[7], SL80_sterr[6]]), SL80_sterr[8:-2]], axis=0),
np.concatenate([SL80_ster_rob[4:6], np.array([SL80_ster_rob[7], SL80_ster_rob[6]]), SL80_ster_rob[8:-2]], axis=0),
],
axis=1,
)
SL79_mu = sigmas = np.concatenate(
[
SL79_theta[-2:],
SL79_sterr[-2:],
SL79_ster_rob[-2:]
],
axis=1,
)
Sl80_mu = sigmas = np.concatenate(
[
SL80_theta[-2:],
SL80_sterr[-2:],
SL80_ster_rob[-2:]
],
axis=1,
)
results.iloc[0:4, 0:3] = SL79_frontier
results.iloc[0:4, 3:] = SL80_frontier
results.iloc[4:11, 0:3] = SL79_sigmas
results.iloc[4:11, 3:] = SL80_sigmas
results.iloc[-2:, 0:3] = SL79_mu
results.iloc[-2:, 3:] = Sl80_mu
display(results)| SL79 Est | SL79 St.Er.(OPG) | SL79 St.Er.(Rob) | SL80 Est | SL80 St.Er.(OPG) | SL80 St.Er.(Rob) | |
|---|---|---|---|---|---|---|
| $$\alpha$$ | -2.613 | 0.064 | 0.073 | -2.586 | 0.064 | 0.069 |
| $$\beta_{1}$$ | 0.511 | 0.024 | 0.027 | 0.482 | 0.027 | 0.027 |
| $$\beta_{2}$$ | 0.263 | 0.013 | 0.022 | 0.267 | 0.013 | 0.021 |
| $$\beta_{3}$$ | 0.239 | 0.025 | 0.02 | 0.255 | 0.028 | 0.021 |
| $$\sigma_{u}^{2}$$ | 0.167 | 0.014 | 0.014 | 0.172 | 0.014 | 0.02 |
| $$\Sigma^{2u}$$ | NaN | NaN | NaN | 0.04 | 0.015 | 0.012 |
| $$\Sigma^{3u}$$ | NaN | NaN | NaN | 0.069 | 0.012 | 0.009 |
| $$\Sigma^{22}$$ | 0.206 | 0.007 | 0.015 | 0.243 | 0.01 | 0.024 |
| $$\Sigma^{23}$$ | 0.097 | 0.006 | 0.012 | 0.093 | 0.006 | 0.017 |
| $$\Sigma^{33}$$ | 0.017 | 0.003 | 0.003 | 0.208 | 0.007 | 0.012 |
| $$\sigma^{2}_{v}$$ | 0.568 | 0.08 | 0.123 | 0.014 | 0.003 | 0.002 |
| $$\mu_{2}$$ | 0.568 | 0.08 | 0.123 | 0.649 | 0.09 | 0.121 |
| $$\mu_{3}$$ | -0.004 | 0.145 | 0.123 | 0.134 | 0.161 | 0.129 |
# Remove all previous function and variable definitions before the next exercise
%reset6.2 Exercise 6.2: The APS2A and APS2B Copulas
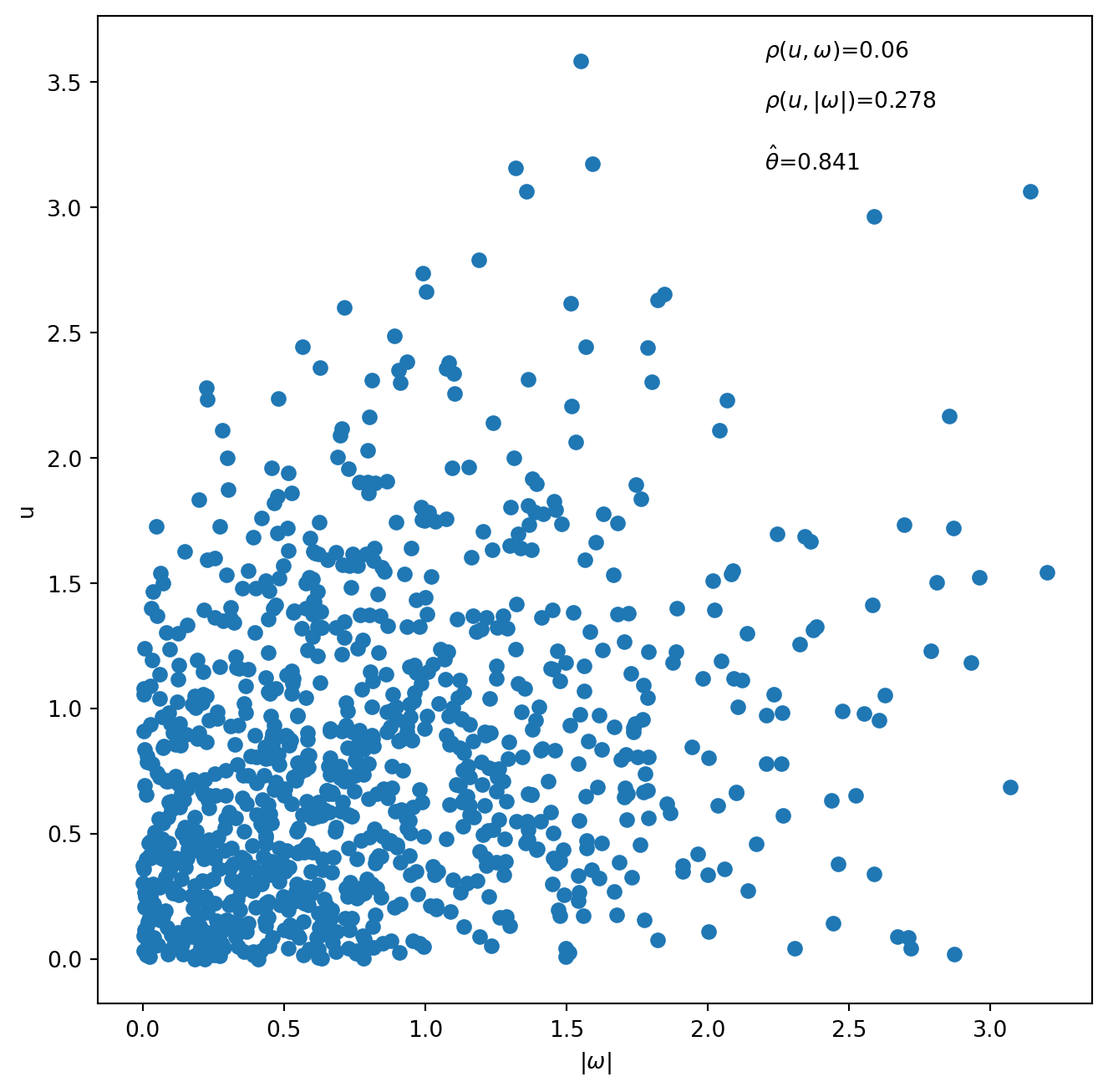
Exercise 6.2 demonstrates how to simulate from and estimate APS2A and APS2B copulas. We generate scatterplots of 1,000 observations simulated using the APS2A and APS2B copulas, respectively. The value of \(\theta\) is set at 0.35 for simulation from APS2A and at 0.8 for simulation from APS2B. We report the correlation between \(u\) and \(\omega\), which is approximately zero, and the correlation between \(u\) and \(|\omega|\) which is positive. We also report the values of \(\theta\) estimated using the MLE on the simulated data.
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
from scipy import stats
def APS2A_deriv_u2(u1, u2, theta):
# Partial derivative of APS2A copula CDF w.r.t second argument
return u1 + theta*u1*(u1 - 1)*(4*u2**2 - 6*u2 + 2) + theta*u1*u2*(8*u2 - 6)*(u1 - 1)
def APS2A_c12_deriv_u2_inverse_func(u2, u1, theta, U):
return APS2A_deriv_u2(u2, u1, theta) - U
def APS2B_deriv_u2(u1, u2, theta):
if u2 <= 0.5:
return u1 - theta*u1*(4*u2 - 1)*(u1 - 1)
else:
return u1 + theta*u1*(4*u2 - 3)*(u1 - 1)
def APS2B_c12_deriv_u2_inverse_func(u2, u1, theta, U):
return APS2B_deriv_u2(u2, u1, theta) - U
def APS2A_loglikelihood(theta, u, w):
F_u = stats.halfnorm.cdf(u)
F_w = stats.norm.cdf(w)
den = 1 + theta*(1-2*F_u)*(1 - 12*(F_w-0.5)**2);
logden = np.log(den)
LL = np.sum(logden)*-1
return LL
def APS2B_loglikelihood(theta, u, w):
F_u = stats.halfnorm.cdf(u)
F_w = stats.norm.cdf(w)
den = 1 + theta*(1-2*F_u)*(1 - 4*np.abs(F_w-0.5))
logden = np.log(den)
LL = np.sum(logden)*-1
return LL#Simulate data from APS2A Copulas
N = 1000
theta = 0.35
np.random.seed(432)
U = np.random.uniform(size=(N, 2))
APS2A_samples = np.zeros((N, 2))
for i in range(N):
APS2A_samples[i,0] = U[i,0]
z2 = optimize.root_scalar(f=APS2A_c12_deriv_u2_inverse_func,
args=(U[i,0], theta, U[i,1]),
bracket=[0, 1])
APS2A_samples[i, 1] = z2.root
APS2A_w = stats.norm.ppf(APS2A_samples[:, 0]);
APS2A_u = 1*stats.norm.ppf((APS2A_samples[:,1]+1)/2) #simulated half normal rvs
display(stats.pearsonr(APS2A_u, APS2A_w)[0])
display(stats.pearsonr(APS2A_u, np.abs(APS2A_w))[0])0.0552592350603418950.20849729680913273# Simulate data from APS2B copulas
np.random.seed(432)
theta = 0.8
U = np.random.uniform(size=(N, 2))
APS2B_samples = np.zeros((N, 2))
for i in range(N):
APS2B_samples[i,0] = U[i,0]
z2 = optimize.root_scalar(f=APS2B_c12_deriv_u2_inverse_func,
args=(U[i,0], theta, U[i,1]),
bracket=[0, 1])
APS2B_samples[i, 1] = z2.root
APS2B_w = stats.norm.ppf(APS2B_samples[:, 0])
APS2B_u = 1*stats.norm.ppf((APS2B_samples[:,1]+1)/2)
display(stats.pearsonr(APS2B_u, APS2B_w)[0])
display(stats.pearsonr(APS2B_u, np.abs(APS2B_w))[0])0.059697973500518920.2775653676762329# Obtain dependence parameters by fitting to data
theta0_APS2A = 0.3
MLE_results = optimize.minimize(fun=APS2A_loglikelihood,
x0=theta0_APS2A,
method="Nelder-Mead",
args=(APS2A_u, APS2A_w))
theta_hat_APS2A = MLE_results.x[0]
logMLE_APS2A = MLE_results.fun
theta0_APS2B = 0.7
MLE_results = optimize.minimize(fun=APS2B_loglikelihood,
x0=theta0_APS2B,
method="Nelder-Mead",
args=(APS2B_u, APS2B_w))
theta_hat_APS2B = MLE_results.x[0]
logMLE_APS2B = MLE_results.fun
fig = plt.figure(figsize=(8, 8))
plt.scatter(np.abs(APS2A_w), APS2A_u)
plt.xlabel(r'$|\omega|$')
plt.ylabel('u')
plt.annotate(text=r'$\rho(u, \omega)$={}'.format(round(stats.pearsonr(APS2A_u, APS2A_w)[0], 3)),
xy=(2.2, 3.6))
plt.annotate(text=r'$\rho(u, |\omega|)$={}'.format(round(stats.pearsonr(APS2A_u, np.abs(APS2A_w))[0], 3)),
xy=(2.2, 3.4))
plt.annotate(text=r'$\hat\theta$={}'.format(round(theta_hat_APS2A, 3)),
xy=(2.2, 3.15))
fig = plt.figure(figsize=(8, 8))
plt.scatter(np.abs(APS2B_w), APS2B_u)
plt.xlabel(r'$|\omega|$')
plt.ylabel('u')
plt.annotate(text=r'$\rho(u, \omega)$={}'.format(round(stats.pearsonr(APS2B_u, APS2B_w)[0], 3)),
xy=(2.2, 3.6))
plt.annotate(text=r'$\rho(u, |\omega|)$={}'.format(round(stats.pearsonr(APS2B_u, np.abs(APS2B_w))[0], 3)),
xy=(2.2, 3.4))
plt.annotate(text=r'$\hat\theta$={}'.format(round(theta_hat_APS2B, 3)),
xy=(2.2, 3.15))Text(2.2, 3.15, '$\\hat\\theta$=0.841')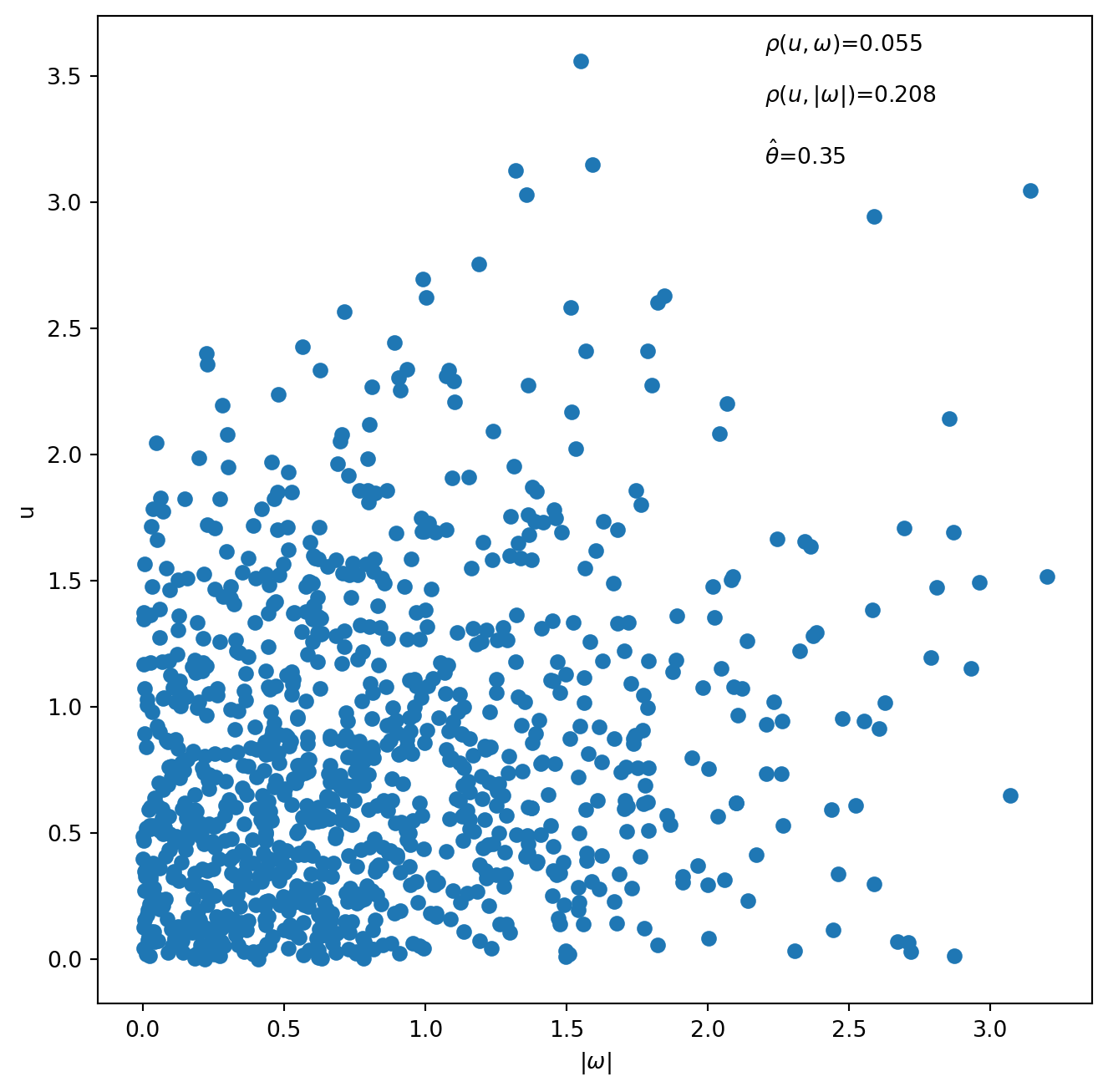
# Remove all previous function and variable definitions before the next exercise
%reset6.3 Exercise 6.3: The APS3A and APS3B estimators for US utilities
This exercise estimates the model in (6.1)-(6.2) using MSLE with the APS- 3-A and APS-3-B copulas on the same dataset as in Exercise 6.1. The number of replications for the simulation of the likelihood is 1,000. The results are similar to each other and to our estimates of the Schmidt and Lovell (1980) model reported in Exercise 6.1. As in Exercise 6.1, “OPG” stands for the expected outer-product of gradient and “Rob” stands for the robust version of the standard errors.
import numpy as np
import pandas as pd
import numdifftools as nd
import copy
from scipy import stats
from scipy.optimize import minimize
def MatrixToCholeski(Sigma):
SigmaChol = np.linalg.cholesky(Sigma)
CholOfSigma = SigmaChol[np.tril_indices(SigmaChol.shape[0], k=0)] # elements of lower triangle of the choleski
return CholOfSigma
def CholeskiToMatrix(CholOfSigma):
SigmaChol = np.zeros((2,2))
SigmaChol[np.tril_indices(SigmaChol.shape[0], k=0)] = CholOfSigma
Sigma = SigmaChol@SigmaChol.T
return Sigma
def transform_parameters(theta):
transformed_theta = copy.deepcopy(theta)
Sigma = CholeskiToMatrix(theta[6:9])
transformed_theta[6:9] = Sigma[np.tril_indices(Sigma.shape[0], k=0)]
return transformed_theta
def AppLoglikelihood_APS3A_FMLE(theta, y, X, P, us):
theta = transform_parameters(theta=theta)
logDen = AppLogDen_APS3A_FMLE(theta, y, X, P, us)
logL = -np.sum(logDen)
return logL
def AppLogDen_APS3A_FMLE(theta, y, X, P, us):
N = len(y)
S = len(us)
[alpha, beta1, beta2, beta3, beta4] = theta[:5]
sigma2u = theta[4]
sigma2v = theta[5]
SigmaWW = np.zeros((2,2))
SigmaWW[np.tril_indices(SigmaWW.shape[0], k=0)] = theta[6:9]
SigmaWW = SigmaWW + SigmaWW.T-np.diag(np.diag(SigmaWW))
theta12 = theta[9]
theta13 = theta[10]
mu = theta[-2:]
eps = y - alpha - X[:,0] * beta1 - X[:,1] * beta2 - X[:,2] * beta3
B2 = P[:,1] - P[:,0] + np.log(beta1) - np.log(beta2)
B3 = P[:,2] - P[:,0] + np.log(beta1) - np.log(beta3)
w2 = X[:,0] - X[:,1] - B2
w3 = X[:,0] - X[:,2] - B3
w = np.array([w2, w3]).T
DenW2 = stats.norm.pdf(w2, mu[0], np.sqrt(SigmaWW[0,0]))
DenW3 = stats.norm.pdf(w3, mu[1], np.sqrt(SigmaWW[1,1]))
CdfW2 = stats.norm.cdf(w2, mu[0], np.sqrt(SigmaWW[0,0]))
CdfW3 = stats.norm.cdf(w3, mu[1], np.sqrt(SigmaWW[1,1]))
CdfUs = 2*(stats.norm.cdf(np.sqrt(sigma2u)*us, 0, np.sqrt(sigma2u)) -0.5);
eps_SxN = np.repeat(eps.reshape(-1,1), S, axis=1).T
us_SxN = np.repeat(np.sqrt(sigma2u)*us.reshape(-1,1), N, axis=1)
EpsPlusUs = eps_SxN + us_SxN
DenEpsPlusUs = stats.norm.pdf(EpsPlusUs, 0, np.sqrt(sigma2v));
w2s_SxN = np.repeat(CdfW2.reshape(-1,1), S, axis=1).T
w3s_SxN = np.repeat(CdfW3.reshape(-1,1), S, axis=1).T
w1s_SxN = np.repeat(CdfUs, N, axis=1)
c12_SxN = 1 + theta12*(1-2*w1s_SxN)*(1-12*(w2s_SxN -0.5)**2)
c13_SxN = 1 + theta13*(1-2*w1s_SxN)*(1-12*(w3s_SxN -0.5)**2)
c23 = stats.multivariate_normal.pdf(w, mean=mu, cov=SigmaWW)/(DenW2*DenW3)
c23_SxN = np.repeat(c23.reshape(-1,1), S, axis=1).T
cstar = 1+(c12_SxN-1)+(c13_SxN-1)+(c23_SxN-1)
Integral = np.mean(cstar*DenEpsPlusUs, axis=0)
DenAll = DenW2*DenW3*Integral
r = beta1+beta2+beta3;
logDen = np.log(r)+np.log(DenAll)
return logDen
def AppEstimate_APS3A_FMLE(y, X, P):
S = 1000 # No. simulated draws for the integral
np.random.seed(12345)
us = stats.norm.ppf((np.random.uniform(size=(S, 1))+1)/2, 0, 1)
alpha = -2.6
beta1 = 0.5
beta2 = 0.2
beta3 = 0.2
sigma2u = 0.14
sigma2v = 0.01
theta12 = -0.1
theta13 = -0.1
sigma22 = 0.337
sigma33 = 0.59
sigma23 = 0.20
mu2 = 0.3
mu3 = 0.3
mu = [mu2, mu3]
SigmaWW = np.array([[sigma22, sigma23],
[sigma23, sigma33]])
CholOfSigma = MatrixToCholeski(SigmaWW) # vector of lower triange of chol of SigmaWW
theta0 = np.array([alpha, beta1, beta2, beta3, sigma2u, sigma2v] + CholOfSigma.tolist() + [theta12, theta13] + mu)
# Bounds to ensure sigma are positive
bounds = [(None, None) for x in range(4)] + [(1e-6, np.inf) for i in range(2)] + [(None, None) for x in range(len(CholOfSigma)+4)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(AppLoglikelihood_APS3A_FMLE,
theta0,
method="Nelder-Mead",
tol = 1e-6,
bounds=bounds,
options={"maxiter": 3000},
args=(y.values, X.values, P.values, us))
# transform parameters
theta_ = MLE_results.x
theta = transform_parameters(theta=theta_)
logMLE = MLE_results.fun * -1 # Log-likelihood at the solution
# standard errors
# gradient calculation
delta = 1e-6
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = np.copy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_APS3A_FMLE(theta1, y.values, X.values, P.values, us) - AppLogDen_APS3A_FMLE(theta, y.values, X.values, P.values, us))/delta
# Hessian calculation
hessian = nd.Hessian(f=AppLoglikelihood_APS3A_FMLE, method="central", step=1e-6)(theta_, y.values, X.values, P.values, us)
# Hessian transformation
D = np.eye(len(theta_))
for i in range(len(theta_)):
theta1 = copy.deepcopy(theta_)
theta1[i] = theta_[i] + delta
D[:,i] = (transform_parameters(theta1)-transform_parameters(theta_))/delta
OPG = grad.T@grad
# Delta method
ster_OPG = np.sqrt(np.diag(np.linalg.inv(OPG)))
ster_rob = np.sqrt(np.diag(D.T@np.linalg.inv(hessian)@D@OPG@D.T@np.linalg.inv(hessian)@D))
return theta, ster_OPG, ster_rob, logMLE
def AppLoglikelihood_APS3B_FMLE(theta, y, X, P, us):
theta = transform_parameters(theta=theta)
logDen = AppLogDen_APS3B_FMLE(theta, y, X, P, us)
logL = -np.sum(logDen)
return logL
def AppLogDen_APS3B_FMLE(theta, y, X, P, us):
N = len(y)
S = len(us)
[alpha, beta1, beta2, beta3, beta4] = theta[:5]
sigma2u = theta[4]
sigma2v = theta[5]
SigmaWW = np.zeros((2,2))
SigmaWW[np.tril_indices(SigmaWW.shape[0], k=0)] = theta[6:9]
SigmaWW = SigmaWW + SigmaWW.T-np.diag(np.diag(SigmaWW))
theta12 = theta[9]
theta13 = theta[10]
mu = theta[-2:]
eps = y - alpha - X[:,0] * beta1 - X[:,1] * beta2 - X[:,2] * beta3
B2 = P[:,1] - P[:,0] + np.log(beta1) - np.log(beta2)
B3 = P[:,2] - P[:,0] + np.log(beta1) - np.log(beta3)
w2 = X[:,0] - X[:,1] - B2
w3 = X[:,0] - X[:,2] - B3
w = np.array([w2, w3]).T
DenW2 = stats.norm.pdf(w2, mu[0], np.sqrt(SigmaWW[0,0]))
DenW3 = stats.norm.pdf(w3, mu[1], np.sqrt(SigmaWW[1,1]))
CdfW2 = stats.norm.cdf(w2, mu[0], np.sqrt(SigmaWW[0,0]))
CdfW3 = stats.norm.cdf(w3, mu[1], np.sqrt(SigmaWW[1,1]))
CdfUs = 2*(stats.norm.cdf(np.sqrt(sigma2u)*us, 0, np.sqrt(sigma2u)) -0.5);
eps_SxN = np.repeat(eps.reshape(-1,1), S, axis=1).T
us_SxN = np.repeat(np.sqrt(sigma2u)*us.reshape(-1,1), N, axis=1)
EpsPlusUs = eps_SxN + us_SxN
DenEpsPlusUs = stats.norm.pdf(EpsPlusUs, 0, np.sqrt(sigma2v));
w2s_SxN = np.repeat(CdfW2.reshape(-1,1), S, axis=1).T
w3s_SxN = np.repeat(CdfW3.reshape(-1,1), S, axis=1).T
w1s_SxN = np.repeat(CdfUs, N, axis=1)
c12_SxN = 1 + theta12*(1-2*w1s_SxN)*(1-4*np.abs(w2s_SxN -0.5))
c13_SxN = 1 + theta13*(1-2*w1s_SxN)*(1-4*np.abs(w3s_SxN -0.5))
c23 = stats.multivariate_normal.pdf(w, mean=mu, cov=SigmaWW)/(DenW2*DenW3)
c23_SxN = np.repeat(c23.reshape(-1,1), S, axis=1).T
cstar = 1+(c12_SxN-1)+(c13_SxN-1)+(c23_SxN-1)
Integral = np.mean(cstar*DenEpsPlusUs, axis=0)
DenAll = DenW2*DenW3*Integral
r = beta1+beta2+beta3;
logDen = np.log(r)+np.log(DenAll)
return logDen
def AppEstimate_APS3B_FMLE(y, X, P):
S = 1000 # No. simulated draws for the integral
np.random.seed(12345)
us = stats.norm.ppf((np.random.uniform(size=(S, 1))+1)/2, 0, 1)
alpha = -2.6
beta1 = 0.5
beta2 = 0.2
beta3 = 0.2
sigma2u = 0.14
sigma2v = 0.01
theta12 = -0.1
theta13 = -0.1
sigma22 = 0.337
sigma33 = 0.59
sigma23 = 0.20
mu2 = 0.3
mu3 = 0.3
mu = [mu2, mu3]
SigmaWW = np.array([[sigma22, sigma23],
[sigma23, sigma33]])
CholOfSigma = MatrixToCholeski(SigmaWW) # vector of lower triange of chol of SigmaWW
theta0 = np.array([alpha, beta1, beta2, beta3, sigma2u, sigma2v] + CholOfSigma.tolist() + [theta12, theta13] + mu)
# Bounds to ensure sigma are positive
bounds = [(None, None) for x in range(4)] + [(1e-6, np.inf) for i in range(2)] + [(None, None) for x in range(len(CholOfSigma)+4)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(AppLoglikelihood_APS3B_FMLE,
theta0,
method="Nelder-Mead",
tol = 1e-6,
bounds=bounds,
options={"maxiter": 3000},
args=(y.values, X.values, P.values, us))
# transform parameters
theta_ = MLE_results.x
theta = transform_parameters(theta=theta_)
logMLE = MLE_results.fun * -1 # Log-likelihood at the solution
# standard errors
# gradient calculation
delta = 1e-6
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = np.copy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_APS3B_FMLE(theta1, y.values, X.values, P.values, us) - AppLogDen_APS3B_FMLE(theta, y.values, X.values, P.values, us))/delta
# Hessian calculation
hessian = nd.Hessian(f=AppLoglikelihood_APS3B_FMLE, method="central", step=1e-6)(theta_, y.values, X.values, P.values, us)
# Hessian transformation
D = np.eye(len(theta_))
for i in range(len(theta_)):
theta1 = copy.deepcopy(theta_)
theta1[i] = theta_[i] + delta
D[:,i] = (transform_parameters(theta1)-transform_parameters(theta_))/delta
OPG = grad.T@grad
# Delta method
ster_OPG = np.sqrt(np.diag(np.linalg.inv(OPG)))
ster_rob = np.sqrt(np.diag(D.T@np.linalg.inv(hessian)@D@OPG@D.T@np.linalg.inv(hessian)@D))
return theta, ster_OPG, ster_rob, logMLE# import data
data = pd.read_excel('steamelectric.xlsx')
data['fuel_price_index'] = np.nan
data.iloc[:-1, -1] = data.iloc[:-1, 2].values/data.iloc[1:,2].values
data['LM_price_index'] = np.nan
data.iloc[:-1, -1] = data.iloc[:-1, 3].values/data.iloc[1:,3].values
data.iloc[13:1007:14, :] = np.nan #drop last fuel price index for each plant
data = data.dropna()
X1 = (data['Fuel Costs ($1000)']/data['fuel_price_index'])*1000*1e-6; #fuel costs over price index
X2 = data['Operating Costs ($1000)']/data['LM_price_index']*1000*1e-6; #LM costs over price index
X3 = data['Capital ($1000)']/1000; # capital
X = np.log(pd.concat([X1, X2, X3], axis=1))
P = np.log(data[['fuel_price_index', 'LM_price_index', 'User Cost of Capital']])
y = np.log(data['Output (MWhr)']*1e-6) # output ml MWpH # import data
data = pd.read_excel('steamelectric.xlsx')
data['fuel_price_index'] = np.nan
data.iloc[:-1, -1] = data.iloc[:-1, 2].values/data.iloc[1:,2].values
data['LM_price_index'] = np.nan
data.iloc[:-1, -1] = data.iloc[:-1, 3].values/data.iloc[1:,3].values
data.iloc[13:1007:14, :] = np.nan #drop last fuel price index for each plant
data = data.dropna()
X1 = (data['Fuel Costs ($1000)']/data['fuel_price_index'])*1000*1e-6; #fuel costs over price index
X2 = data['Operating Costs ($1000)']/data['LM_price_index']*1000*1e-6; #LM costs over price index
X3 = data['Capital ($1000)']/1000; # capital
X = np.log(pd.concat([X1, X2, X3], axis=1))
P = np.log(data[['fuel_price_index', 'LM_price_index', 'User Cost of Capital']])
y = np.log(data['Output (MWhr)']*1e-6) # output ml MWpH
APS3A_theta, APS3A_ster_OPG, APS3A_ster_rob, APS3A_logMLE = AppEstimate_APS3A_FMLE(y=y, X=X, P=P)
APS3B_theta, APS3B_ster_OPG, APS3B_ster_rob, APS3B_logMLE = AppEstimate_APS3B_FMLE(y=y, X=X, P=P)
# Display the results as a table
results = pd.DataFrame(
columns=["AS3A Est", "AS3A St.Er.(OPG)", "AS3A St.Er.(Rob)",
"AS3B Est", "AS3B St.Er.(OPG)", "AS3B St.Er.(Rob)"],
index=[
r"$$\alpha$$",
r"$$\beta_{1}$$",
r"$$\beta_{2}$$",
r"$$\beta_{3}$$",
r"$$\sigma_{u}^{2}$$",
r"$$\Sigma^{22}$$",
r"$$\Sigma^{23}$$",
r"$$\Sigma^{33}$$",
r"$$\sigma^{2}_{v}$$",
r"$$\mu_{2}$$",
r"$$\mu_{3}$$",
r"$$\theta_{12}$$",
r"$$\theta_{13}$$"
],
)
APS3A_theta = np.round(APS3A_theta.reshape(-1, 1), 3)
APS3A_ster_OPG = np.round(APS3A_ster_OPG.reshape(-1, 1), 3)
APS3A_ster_rob = np.round(APS3A_ster_rob.reshape(-1, 1), 3)
APS3B_theta = np.round(APS3B_theta.reshape(-1, 1), 3)
APS3B_ster_OPG = np.round(APS3B_ster_OPG.reshape(-1, 1), 3)
APS3B_ster_rob = np.round(APS3B_ster_rob.reshape(-1, 1), 3)
APS3A_frontier = np.concatenate(
[
APS3A_theta[:4],
APS3A_ster_OPG[:4],
APS3A_ster_rob[:4]
],
axis=1,
)
APS3B_frontier = np.concatenate(
[
APS3B_theta[:4],
APS3B_ster_OPG[:4],
APS3B_ster_rob[:4]
],
axis=1,
)
APS3A_sigmas = np.concatenate(
[
np.concatenate([APS3A_theta[[4]], APS3A_theta[6:9], APS3A_theta[[5]]], axis=0),
np.concatenate([APS3A_ster_OPG[[4]], APS3A_ster_OPG[6:9], APS3A_ster_OPG[[5]]], axis=0),
np.concatenate([APS3A_ster_rob[[4]], APS3A_ster_rob[6:9], APS3A_ster_rob[[5]]], axis=0),
],
axis=1,
)
APS3B_sigmas = np.concatenate(
[
np.concatenate([APS3B_theta[[4]], APS3B_theta[6:9], APS3B_theta[[5]]], axis=0),
np.concatenate([APS3B_ster_OPG[[4]], APS3B_ster_OPG[6:9], APS3B_ster_OPG[[5]]], axis=0),
np.concatenate([APS3B_ster_rob[[4]], APS3B_ster_rob[6:9], APS3B_ster_rob[[5]]], axis=0),
],
axis=1,
)
APS3A_thetas = np.concatenate(
[
APS3A_theta[-4:-2],
APS3A_ster_OPG[-4:-2],
APS3A_ster_rob[-4:-2]
],
axis=1,
)
APS3B_thetas = np.concatenate(
[
APS3B_theta[-4:-2],
APS3B_ster_OPG[-4:-2],
APS3B_ster_rob[-4:-2]
],
axis=1,
)
APS3A_mu = sigmas = np.concatenate(
[
APS3A_theta[-2:],
APS3A_ster_OPG[-2:],
APS3A_ster_rob[-2:]
],
axis=1,
)
APS3B_mu = sigmas = np.concatenate(
[
APS3B_theta[-2:],
APS3B_ster_OPG[-2:],
APS3B_ster_rob[-2:]
],
axis=1,
)
results.iloc[0:4, 0:3] = APS3A_frontier
results.iloc[0:4, 3:] = APS3B_frontier
results.iloc[4:9, 0:3] = APS3A_sigmas
results.iloc[4:9, 3:] = APS3B_sigmas
results.iloc[9:11, 0:3] = APS3A_mu
results.iloc[9:11, 3:] = APS3B_mu
results.iloc[-2:, 0:3] = APS3A_thetas
results.iloc[-2:, 3:] = APS3B_thetas
display(results)/var/folders/q0/9kb46g7n1_57dfk7vtdsv8t4w169ch/T/ipykernel_8109/1901131725.py:96: RuntimeWarning: invalid value encountered in log
logDen = np.log(r)+np.log(DenAll)/var/folders/q0/9kb46g7n1_57dfk7vtdsv8t4w169ch/T/ipykernel_8109/1901131725.py:235: RuntimeWarning: invalid value encountered in log
logDen = np.log(r)+np.log(DenAll)| AS3A Est | AS3A St.Er.(OPG) | AS3A St.Er.(Rob) | AS3B Est | AS3B St.Er.(OPG) | AS3B St.Er.(Rob) | |
|---|---|---|---|---|---|---|
| $$\alpha$$ | -2.733 | 0.068 | 0.1 | -2.731 | 0.062 | 0.069 |
| $$\beta_{1}$$ | 0.544 | 0.025 | 0.039 | 0.493 | 0.025 | 0.028 |
| $$\beta_{2}$$ | 0.218 | 0.016 | 0.041 | 0.253 | 0.014 | 0.022 |
| $$\beta_{3}$$ | 0.256 | 0.025 | 0.017 | 0.279 | 0.024 | 0.018 |
| $$\sigma_{u}^{2}$$ | 0.151 | 0.016 | 0.019 | 0.18 | 0.015 | 0.017 |
| $$\Sigma^{22}$$ | 0.249 | 0.011 | 0.021 | 0.247 | 0.01 | 0.02 |
| $$\Sigma^{23}$$ | 0.115 | 0.007 | 0.012 | 0.119 | 0.007 | 0.012 |
| $$\Sigma^{33}$$ | 0.219 | 0.008 | 0.013 | 0.209 | 0.007 | 0.009 |
| $$\sigma^{2}_{v}$$ | 0.024 | 0.005 | 0.006 | 0.018 | 0.004 | 0.003 |
| $$\mu_{2}$$ | 0.306 | 0.099 | 0.251 | 0.562 | 0.089 | 0.132 |
| $$\mu_{3}$$ | -0.001 | 0.134 | 0.1 | 0.181 | 0.128 | 0.109 |
| $$\theta_{12}$$ | -0.198 | 0.032 | 0.034 | -0.28 | 0.062 | 0.057 |
| $$\theta_{13}$$ | -0.035 | 0.058 | 0.065 | -0.088 | 0.077 | 0.077 |
# Remove all previous function and variable definitions before the next exercise
%reset6.4 Exercise 6.4 Vine APS-2-copula estimates for the 111 US utilities.
This exercise estimates the model in (6.1)-(6.2) using MSLE with the vine copulas based on the APS-2-A and APS-2-B copulas. The data file is cowing.xlsx which was also used in Chapter 2. In this exercise we use an approach known as the extended value extension. That is, rather than use a parameter transformation of the correlation matrix we check if the correlation matrix is positive definite within the objective function and return a very large value of the objective if this condition is not met.
Table 6.3 reports the results. We also report the estimates based on the APS3 copula for this dataset. The copula dependence parameter estimates are, for the most part, large in magnitude but statistically insignificant for this example.
import numpy as np
import pandas as pd
import copy
from scipy import stats
from scipy.optimize import minimize
def AppLoglikelihood_APS3A_FMLE(theta, y, X, P, us):
logDen = AppLogDen_APS3A_FMLE(theta, y, X, P, us)
logL = -np.sum(logDen)
return logL
def AppLogDen_APS3A_FMLE(theta, y, X, P, us):
n = len(y)
S = len(us)
[alpha, beta1, beta2, beta3, mu2, mu3, sigma2u, sigma2v,
sigma2w2, sigma2w3, pw1w2, theta12, theta13] = theta[:]
eps = y - alpha - X[:,0] * beta1 - X[:,1] * beta2 - X[:,2] * beta3
B2 = P[:,1] - P[:,0] + np.log(beta1) - np.log(beta2)
B3 = P[:,2] - P[:,0] + np.log(beta1) - np.log(beta3)
w2 = X[:,0] - X[:,1] - B2
w3 = X[:,0] - X[:,2] - B3
CdfUs = 2*(stats.norm.cdf(np.sqrt(sigma2u)*us, 0, np.sqrt(sigma2u)) -0.5)
eps_SxN = np.repeat(eps.reshape(-1,1), S, axis=1).T
us_SxN = np.sqrt(sigma2u)*us
EpsPlusUs = eps_SxN + us_SxN
DenEpsPlusUs = stats.norm.pdf(EpsPlusUs, 0, np.sqrt(sigma2v))
RhoWW =np.array([[1,pw1w2],
[pw1w2,1]])
# Check Rho
if not np.all(np.linalg.eigvals(RhoWW) > 0):
logDen = np.ones((n, 1))*-1e8
else:
# Evaluate the integral via simulation (to integrate out u from eps+u)
simulated_copula_pdfs = np.zeros(us_SxN.shape)
DenW2 = stats.norm.pdf(w2, mu2, np.sqrt(sigma2w2))
DenW3 = stats.norm.pdf(w3, mu3, np.sqrt(sigma2w3))
w2_rep = np.repeat(w2.reshape(-1,1), S, axis=1).T
w3_rep = np.repeat(w3.reshape(-1,1), S, axis=1).T
# Compute the CDF (standard normal) for repeated allocative inefficiency terms
CDF_w2_rep = stats.norm.cdf(w2_rep, mu2, np.sqrt(sigma2w2))
CDF_w3_rep = stats.norm.cdf(w3_rep, mu3, np.sqrt(sigma2w3))
for j in range(n):
simulated_c12_pdf = 1 + theta12*(1-2*CdfUs[:,j])*(1 - 12*(CDF_w2_rep[:,j] - 0.5)**2)
simulated_c13_pdf = 1 + theta13*(1-2*CdfUs[:,j])*(1 - 12*(CDF_w3_rep[:,j] - 0.5)**2)
U = np.concatenate([stats.norm.ppf(CDF_w2_rep[:, j]).reshape(-1,1),
stats.norm.ppf(CDF_w3_rep[:, j]).reshape(-1,1)],
axis=1)
simulated_c23_pdf = stats.multivariate_normal.pdf(U, mean = np.array([0, 0]), cov=RhoWW)/ np.prod(stats.norm.pdf(U), axis=1)
APS3A_copula_pdf = 1 + (simulated_c12_pdf -1) + (simulated_c13_pdf - 1) + (simulated_c23_pdf - 1)
simulated_copula_pdfs[:,j] = APS3A_copula_pdf
Integral = np.mean(simulated_copula_pdfs*DenEpsPlusUs, axis=0)
DenAll = DenW2*DenW3*Integral
r = beta1 + beta2 + beta3
logDen = np.log(r) + np.log(DenAll)
return logDen
def AppEstimate_APS3A_FMLE(y, X, P):
n = len(y)
S = 100 # No. simulated draws for the integral
np.random.seed(12345)
us = stats.norm.ppf((np.random.uniform(size=(S, n))+1)/2, 0, 1)
# Starting values for MLE
initial_alpha = -11.6
initial_beta1 = 0.06
initial_beta2 = 1.04
initial_beta3 = 0.06
initial_sigma2u = 0.014
initial_sigma2v = 0.002
initial_theta12 = 0 # APS c12 copula parameter
initial_theta13 = 0 # APS c13 copula parameter
initial_sigma2w2 = 0.33 # variance of w2
initial_sigma2w3 = 0.59 # variance of w3
initial_mu2 = 1.3 # mean of normal distribution for w1
initial_mu3 = 1 #mean of normal distribution for w2
# Find starting value for rho in gaussian copula for w1w2
B2 = P.iloc[:,1] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta2)
B3 = P.iloc[:,2] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta3)
w2 = X.iloc[:, 0] - X.iloc[:, 1] - B2
w3 = X.iloc[:, 0] - X.iloc[:, 2] - B3
initial_pw1w2 = stats.kendalltau(x=stats.norm.cdf(w2, initial_mu2, np.sqrt(initial_sigma2w2)),
y=stats.norm.cdf(w3, initial_mu3, np.sqrt(initial_sigma2w2)))[0]
theta0 = [initial_alpha, initial_beta1, initial_beta2, initial_beta3,
initial_mu2, initial_mu3,
initial_sigma2u, initial_sigma2v, initial_sigma2w2,
initial_sigma2w3, initial_pw1w2, initial_theta12, initial_theta13]
# Bounds to ensure sigma2v and sigma2u are >= 0
bounds = [(None, None) for x in range(6)] + [
(1e-5, np.inf),
(1e-5, np.inf),
] + [(None, None) for x in range(5)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(
fun=AppLoglikelihood_APS3A_FMLE,
x0=theta0,
method="L-BFGS-B",
tol = 1e-6,
options={"ftol": 1e-6, "maxiter": 1000, "maxfun": 6*1000},
args=(y.values, X.values, P.values, us),
bounds=bounds,
)
theta = MLE_results.x
logMLE = MLE_results.fun * -1 # Log-likelihood at the solution
# Estimation of standard errors
delta = 1e-6;
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = copy.deepcopy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_APS3A_FMLE(theta1, y.values, X.values, P.values, us) - AppLogDen_APS3A_FMLE(theta, y.values, X.values, P.values, us))/delta
OPG = grad.T@grad # Outer product of the gradient
sterr = np.sqrt(np.diag(np.linalg.inv(OPG)))
return theta, sterr, logMLE
def AppLoglikelihood_APS3B_FMLE(theta, y, X, P, us):
logDen = AppLogDen_APS3B_FMLE(theta, y, X, P, us)
logL = -np.sum(logDen)
return logL
def AppLogDen_APS3B_FMLE(theta, y, X, P, us):
n = len(y)
S = len(us)
[alpha, beta1, beta2, beta3, mu2, mu3, sigma2u, sigma2v,
sigma2w2, sigma2w3, pw1w2, theta12, theta13] = theta[:]
eps = y - alpha - X[:,0] * beta1 - X[:,1] * beta2 - X[:,2] * beta3
B2 = P[:,1] - P[:,0] + np.log(beta1) - np.log(beta2)
B3 = P[:,2] - P[:,0] + np.log(beta1) - np.log(beta3)
w2 = X[:,0] - X[:,1] - B2
w3 = X[:,0] - X[:,2] - B3
CdfUs = 2*(stats.norm.cdf(np.sqrt(sigma2u)*us, 0, np.sqrt(sigma2u)) -0.5)
eps_SxN = np.repeat(eps.reshape(-1,1), S, axis=1).T
us_SxN = np.sqrt(sigma2u)*us
EpsPlusUs = eps_SxN + us_SxN
DenEpsPlusUs = stats.norm.pdf(EpsPlusUs, 0, np.sqrt(sigma2v))
RhoWW =np.array([[1,pw1w2],
[pw1w2,1]])
# Check Rho
if not np.all(np.linalg.eigvals(RhoWW) > 0):
logDen = np.ones((n, 1))*-1e8
else:
# Evaluate the integral via simulation (to integrate out u from eps+u)
simulated_copula_pdfs = np.zeros(us_SxN.shape)
DenW2 = stats.norm.pdf(w2, mu2, np.sqrt(sigma2w2))
DenW3 = stats.norm.pdf(w3, mu3, np.sqrt(sigma2w3))
w2_rep = np.repeat(w2.reshape(-1,1), S, axis=1).T
w3_rep = np.repeat(w3.reshape(-1,1), S, axis=1).T
# Compute the CDF (standard normal) for repeated allocative inefficiency terms
CDF_w2_rep = stats.norm.cdf(w2_rep, mu2, np.sqrt(sigma2w2))
CDF_w3_rep = stats.norm.cdf(w3_rep, mu3, np.sqrt(sigma2w3))
for j in range(n):
simulated_c12_pdf = 1 + theta12*(1-2*CdfUs[:,j])*(1 - 4*abs(CDF_w2_rep[:,j]-0.5))
simulated_c13_pdf = 1 + theta13*(1-2*CdfUs[:,j])*(1-4*abs(CDF_w3_rep[:,j] - 0.5))
U = np.concatenate([stats.norm.ppf(CDF_w2_rep[:, j]).reshape(-1,1),
stats.norm.ppf(CDF_w3_rep[:, j]).reshape(-1,1)],
axis=1)
simulated_c23_pdf = stats.multivariate_normal.pdf(U, mean = np.array([0, 0]), cov=RhoWW)/ np.prod(stats.norm.pdf(U), axis=1)
APS3A_copula_pdf = 1 + (simulated_c12_pdf -1) + (simulated_c13_pdf - 1) + (simulated_c23_pdf - 1)
simulated_copula_pdfs[:,j] = APS3A_copula_pdf
Integral = np.mean(simulated_copula_pdfs*DenEpsPlusUs, axis=0)
DenAll = DenW2*DenW3*Integral
r = beta1 + beta2 + beta3
logDen = np.log(r) + np.log(DenAll)
return logDen
def AppEstimate_APS3B_FMLE(y, X, P):
n = len(y)
S = 100 # No. simulated draws for the integral
np.random.seed(12345)
us = stats.norm.ppf((np.random.uniform(size=(S, n))+1)/2, 0, 1)
# Starting values for MLE
initial_alpha = -11.6
initial_beta1 = 0.06
initial_beta2 = 1.04
initial_beta3 = 0.06
initial_sigma2u = 0.014
initial_sigma2v = 0.002
initial_theta12 = 0 # APS c12 copula parameter
initial_theta13 = 0 # APS c13 copula parameter
initial_sigma2w2 = 0.33 # variance of w2
initial_sigma2w3 = 0.59 # variance of w3
initial_mu2 = 1.3 # mean of normal distribution for w1
initial_mu3 = 1 #mean of normal distribution for w2
# Find starting value for rho in gaussian copula for w1w2
B2 = P.iloc[:,1] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta2)
B3 = P.iloc[:,2] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta3)
w2 = X.iloc[:, 0] - X.iloc[:, 1] - B2
w3 = X.iloc[:, 0] - X.iloc[:, 2] - B3
initial_pw1w2 = stats.kendalltau(x=stats.norm.cdf(w2, initial_mu2, np.sqrt(initial_sigma2w2)),
y=stats.norm.cdf(w3, initial_mu3, np.sqrt(initial_sigma2w2)))[0]
theta0 = [initial_alpha, initial_beta1, initial_beta2, initial_beta3,
initial_mu2, initial_mu3,
initial_sigma2u, initial_sigma2v, initial_sigma2w2,
initial_sigma2w3, initial_pw1w2, initial_theta12, initial_theta13]
# Bounds to ensure sigma2v and sigma2u are >= 0
bounds = [(None, None) for x in range(6)] + [
(1e-5, np.inf),
(1e-5, np.inf),
] + [(None, None) for x in range(5)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(
fun=AppLoglikelihood_APS3B_FMLE,
x0=theta0,
method="L-BFGS-B",
tol = 1e-6,
options={"ftol": 1e-6, "maxiter": 1000, "maxfun": 6*1000},
args=(y.values, X.values, P.values, us),
bounds=bounds,
)
theta = MLE_results.x
logMLE = MLE_results.fun * -1 # Log-likelihood at the solution
# Estimation of standard errors
delta = 1e-6;
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = copy.deepcopy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_APS3B_FMLE(theta1, y.values, X.values, P.values, us) - AppLogDen_APS3B_FMLE(theta, y.values, X.values, P.values, us))/delta
OPG = grad.T@grad # Outer product of the gradient
sterr = np.sqrt(np.diag(np.linalg.inv(OPG)))
return theta, sterr, logMLE
def AppLogDen_Vine_APS2A(theta, y, X, P, us):
N = len(y)
S, p = us.shape
[alpha, beta1, beta2, beta3, mu2, mu3, sigma2u, sigma2v,
sigma2w2, sigma2w3, pw1w2, theta12, theta13] = theta[:]
eps = y - alpha - X[:, 0]*beta1 - X[:, 1]*beta2 - X[:, 2]*beta3
B2 = P[:,1] - P[:,0] + np.log(beta1) - np.log(beta2)
B3 = P[:,2] - P[:,0] + np.log(beta1) - np.log(beta3)
w2 = X[:,0] - X[:,1] - B2
w3 = X[:,0] - X[:,2] - B3
CdfUs = 2*(stats.norm.cdf(np.sqrt(sigma2u)*us, 0, np.sqrt(sigma2u)) -0.5)
eps_SxN = np.repeat(eps.reshape(-1,1), S, axis=1).T
us_SxN = np.sqrt(sigma2u)*us
EpsPlusUs = eps_SxN + us_SxN
DenEpsPlusUs = stats.norm.pdf(EpsPlusUs, 0, np.sqrt(sigma2v))
DenW2 = stats.norm.pdf(w2, mu2, np.sqrt(sigma2w2))
DenW3 = stats.norm.pdf(w3, mu3, np.sqrt(sigma2w3))
RhoWW =np.array([[1,pw1w2],
[pw1w2,1]])
# Check Rho
if not np.all(np.linalg.eigvals(RhoWW) > 0):
logDen = np.ones((N, 1))*-1e8
else:
# Evaluate the integral via simulation (to integrate out u from eps+u)
simulated_copula_pdfs = np.zeros(us_SxN.shape)
w2_rep = np.repeat(w2.reshape(-1,1), S, axis=1).T
w3_rep = np.repeat(w3.reshape(-1,1), S, axis=1).T
# Compute the CDF (standard normal) for repeated allocative inefficiency terms
CDF_w2_rep = stats.norm.cdf(w2_rep, mu2, np.sqrt(sigma2w2))
CDF_w3_rep = stats.norm.cdf(w3_rep, mu3, np.sqrt(sigma2w3))
conditional_CDF_w2_u = CDF_w2_rep + theta12*CdfUs*CDF_w2_rep*(4*CDF_w2_rep**2 - 6*CDF_w2_rep + 2) + theta12*CDF_w2_rep*(CdfUs - 1)*(4*CDF_w2_rep**2 - 6*CDF_w2_rep + 2)
conditional_CDF_w3_u = CDF_w3_rep + theta13*CdfUs*CDF_w3_rep*(4*CDF_w3_rep**2 - 6*CDF_w3_rep + 2) + theta13*CDF_w3_rep*(CdfUs - 1)*(4*CDF_w3_rep**2 - 6*CDF_w3_rep + 2)
for j in range(N):
simulated_c21_pdf = 1 + theta12*(1-2*CdfUs[:,j])*(1 - 12*(CDF_w2_rep[:,j] - 0.5)**2)
simulated_c31_pdf = 1 + theta13*(1-2*CdfUs[:,j])*(1 - 12*(CDF_w3_rep[:,j] - 0.5)**2)
U = np.concatenate([stats.norm.ppf(conditional_CDF_w2_u[:, j]).reshape(-1,1),
stats.norm.ppf(conditional_CDF_w3_u[:, j]).reshape(-1,1)],
axis=1)
simulated_c23_pdf = stats.multivariate_normal.pdf(U, mean = np.array([0, 0]), cov=RhoWW)/ np.prod(stats.norm.pdf(U), axis=1)
APS2A_copula_pdf = simulated_c21_pdf*simulated_c31_pdf*simulated_c23_pdf
simulated_copula_pdfs[:,j] = APS2A_copula_pdf
Integral = np.mean(simulated_copula_pdfs*DenEpsPlusUs, axis=0)
DenAll = DenW2*DenW3*Integral
r = beta1 + beta2 + beta3
logDen = np.log(r) + np.log(DenAll)
return logDen
def AppLoglikelihood_vine_APS2A(theta, y, X, P, us):
logDen = AppLogDen_Vine_APS2A(theta, y, X, P, us)
logL = -np.sum(logDen)
return logL
def AppEstimate_Vine_APS2A(y, X, P):
# Standard Normal random variables for simulation of the integral.
np.random.seed(12345)
S = 100
n = len(y)
us = stats.norm.ppf((np.random.uniform(size=(S, n))+1)/2, 0, 1)
# Starting values for MLE
initial_alpha = -11.6
initial_beta1 = 0.06
initial_beta2 = 1.04
initial_beta3 = 0.06
initial_sigma2u = 0.014
initial_sigma2v = 0.002
initial_theta12 = 0.2 # APS c12 copula parameter
initial_theta13 = -0.2 # APS c13 copula parameter
initial_sigma2w2 = 0.33 # variance of w2
initial_sigma2w3 = 0.59 # variance of w3
initial_mu2 = 2 # mean of normal distribution for w1
initial_mu3 = 0.5 #mean of normal distribution for w2
# Find starting value for rho in gaussian copula for w1w2
B2 = P.iloc[:,1] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta2)
B3 = P.iloc[:,2] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta3)
w2 = X.iloc[:, 0] - X.iloc[:, 1] - B2
w3 = X.iloc[:, 0] - X.iloc[:, 2] - B3
# Conditional CDF transforms for allocative inefficiency correlation starting value
CDF_simulated_us = 2*(stats.norm.cdf(np.sqrt(initial_sigma2u)*us[0, :], 0, np.sqrt(initial_sigma2u)) -0.5)
CDF_w2 = stats.norm.cdf(w2, initial_mu2, np.sqrt(initial_sigma2w2))
CDF_w3 = stats.norm.cdf(w3, initial_mu3 , np.sqrt(initial_sigma2w3))
APS2A_CDF_w2_conditional_u = CDF_w2 + (initial_theta12*CDF_w2)*(1 - CDF_w2)*(2*(6*CDF_simulated_us - 6*CDF_simulated_us**2 - 1))
APS2A_CDF_w3_conditional_u = CDF_w3 + (initial_theta13*CDF_w3)*(1 - CDF_w3)*(2*(6*CDF_simulated_us - 6*CDF_simulated_us**2 - 1))
initial_pw1w2 = stats.kendalltau(x=APS2A_CDF_w2_conditional_u,
y=APS2A_CDF_w3_conditional_u)[0]
theta0 = [initial_alpha, initial_beta1, initial_beta2, initial_beta3,
initial_mu2, initial_mu3, initial_sigma2u, initial_sigma2v,
initial_sigma2w2, initial_sigma2w3, initial_pw1w2,
initial_theta12, initial_theta13]
# Bounds to ensure sigma2v and sigma2u are >= 0
bounds = [(None, None) for x in range(6)] + [
(1e-5, np.inf),
(1e-5, np.inf),
] + [(None, None) for x in range(5)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(
fun=AppLoglikelihood_vine_APS2A,
x0=theta0,
method="L-BFGS-B",
tol = 1e-6,
options={"ftol": 1e-6, "maxiter": 1000, "maxfun": 6*1000},
args=(y.values, X.values, P.values, us),
bounds=bounds,
)
theta = MLE_results.x # Estimated parameter vector
log_likelihood = MLE_results.fun * -1 # Log-likelihood at the solution
# Estimation of standard errors
delta = 1e-6;
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = copy.deepcopy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_Vine_APS2A(theta1, y.values, X.values, P.values, us) - AppLogDen_Vine_APS2A(theta, y.values, X.values, P.values, us))/delta
OPG = grad.T@grad # Outer product of the gradient
sterr = np.sqrt(np.diag(np.linalg.inv(OPG)))
return theta, sterr, log_likelihood
def AppLogDen_Vine_APS2B(theta, y, X, P, us):
n = len(y)
S, p = us.shape
[alpha, beta1, beta2, beta3, mu2, mu3, sigma2u, sigma2v,
sigma2w2, sigma2w3, pw1w2, theta12, theta13] = theta[:]
eps = y - alpha - X[:, 0]*beta1 - X[:, 1]*beta2 - X[:, 2]*beta3
B2 = P[:,1] - P[:,0] + np.log(beta1) - np.log(beta2)
B3 = P[:,2] - P[:,0] + np.log(beta1) - np.log(beta3)
w2 = X[:,0] - X[:,1] - B2
w3 = X[:,0] - X[:,2] - B3
CdfUs = 2*(stats.norm.cdf(np.sqrt(sigma2u)*us, 0, np.sqrt(sigma2u)) -0.5)
eps_SxN = np.repeat(eps.reshape(-1,1), S, axis=1).T
us_SxN = np.sqrt(sigma2u)*us
EpsPlusUs = eps_SxN + us_SxN
DenEpsPlusUs = stats.norm.pdf(EpsPlusUs, 0, np.sqrt(sigma2v))
DenW2 = stats.norm.pdf(w2, mu2, np.sqrt(sigma2w2))
DenW3 = stats.norm.pdf(w3, mu3, np.sqrt(sigma2w3))
RhoWW =np.array([[1,pw1w2],
[pw1w2,1]])
# Check Rho
if not np.all(np.linalg.eigvals(RhoWW) > 0):
logDen = np.ones((n, 1))*-1e8
else:
# Evaluate the integral via simulation (to integrate out u from eps+u)
simulated_copula_pdfs = np.zeros(us_SxN.shape)
w2_rep = np.repeat(w2.reshape(-1,1), S, axis=1).T
w3_rep = np.repeat(w3.reshape(-1,1), S, axis=1).T
# Compute the CDF (standard normal) for repeated allocative inefficiency terms
CDF_w2_rep = stats.norm.cdf(w2_rep, mu2, np.sqrt(sigma2w2))
CDF_w3_rep = stats.norm.cdf(w3_rep, mu3, np.sqrt(sigma2w3))
#Compute the conditional CDFs for allocative inefficiency terms F(w1|u), F(w2|u)
conditional_CDF_w2_u = np.zeros((S, n))
conditional_CDF_w3_u = np.zeros((S, n))
for j in range(n):
if w2[j] <= 0.5:
conditional_CDF_w2_u[:,j] = CDF_w2_rep[:,j] + theta12*CdfUs[:,j]*(-2*CDF_w2_rep[:,j]**2 + CDF_w2_rep[:,j]) + theta12*(-2*CDF_w2_rep[:,j]**2 + CDF_w2_rep[:,j])*(CdfUs[:,j] - 1)
else:
conditional_CDF_w2_u[:,j] = CDF_w2_rep[:,j] + theta12*(CdfUs[:,j] - 1)*(2*CDF_w2_rep[:,j]**2 - 3*CDF_w2_rep[:,j] + 1) + theta12*CdfUs[:,j]*(2*CDF_w2_rep[:,j]**2 - 3*CDF_w2_rep[:,j] + 1)
if w3[j] <= 0.5:
conditional_CDF_w3_u[:,j] = CDF_w3_rep[:,j] + theta13*CdfUs[:,j]*(-2*CDF_w3_rep[:,j]**2 + CDF_w3_rep[:,j]) + theta13*(-2*CDF_w3_rep[:,j]**2 + CDF_w3_rep[:,j])*(CdfUs[:,j] - 1)
else:
conditional_CDF_w3_u[:,j] = CDF_w3_rep[:,j] + theta13*(CdfUs[:,j] - 1)*(2*CDF_w3_rep[:,j]**2 - 3*CDF_w3_rep[:,j] + 1) + theta13*CdfUs[:,j]*(2*CDF_w3_rep[:,j]**2 - 3*CDF_w3_rep[:,j] + 1)
simulated_c21_pdf = 1 + theta12*(1-2*CdfUs[:,j])*(1 - 4*np.abs(CDF_w2_rep[:,j] - 0.5))
simulated_c31_pdf = 1 + theta13*(1-2*CdfUs[:,j])*(1-4*np.abs(CDF_w3_rep[:,j] - 0.5))
U = np.concatenate([stats.norm.ppf(conditional_CDF_w2_u[:, j]).reshape(-1,1),
stats.norm.ppf(conditional_CDF_w3_u[:, j]).reshape(-1,1)],
axis=1)
simulated_c23_pdf = stats.multivariate_normal.pdf(U, mean = np.array([0, 0]), cov=RhoWW)/ np.prod(stats.norm.pdf(U), axis=1)
APS2B_copula_pdf = simulated_c21_pdf*simulated_c31_pdf*simulated_c23_pdf
simulated_copula_pdfs[:,j] = APS2B_copula_pdf
Integral = np.mean(simulated_copula_pdfs*DenEpsPlusUs, axis=0)
DenAll = DenW2*DenW3*Integral
r = beta1 + beta2 + beta3
logDen = np.log(r) + np.log(DenAll)
return logDen
def AppLoglikelihood_vine_APS2B(theta, y, X, P, us):
logDen = AppLogDen_Vine_APS2B(theta, y, X, P, us)
logL = -np.sum(logDen)
return logL
def AppEstimate_Vine_APS2B(y, X, P):
# Standard Normal random variables for simulation of the integral.
np.random.seed(12345)
S = 100
n = len(y)
us = stats.norm.ppf((np.random.uniform(size=(S, n))+1)/2, 0, 1)
# Starting values for MLE
initial_alpha = -11.6
initial_beta1 = 0.045
initial_beta2 = 1.04
initial_beta3 = 0.06
initial_sigma2u = 0.014
initial_sigma2v = 0.002
initial_theta12 = 0.1 # APS c12 copula parameter
initial_theta13 = -0.2 # APS c13 copula parameter
initial_sigma2w2 = 0.33 # variance of w2
initial_sigma2w3 = 0.59 # variance of w3
initial_mu2 = 2 # mean of normal distribution for w1
initial_mu3 = 0.5 #mean of normal distribution for w2
# Find starting value for rho in gaussian copula for w1w2
B2 = P.iloc[:,1] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta2)
B3 = P.iloc[:,2] - P.iloc[:,0] + np.log(initial_beta1) - np.log(initial_beta3)
w2 = X.iloc[:, 0] - X.iloc[:, 1] - B2
w3 = X.iloc[:, 0] - X.iloc[:, 2] - B3
# Conditional CDF transforms for allocative inefficiency correlation starting value
CDF_simulated_us = 2*(stats.norm.cdf(np.sqrt(initial_sigma2u)*us[0, :], 0, np.sqrt(initial_sigma2u)) -0.5)
CDF_w2 = stats.norm.cdf(w2, initial_mu2, np.sqrt(initial_sigma2w2))
CDF_w3 = stats.norm.cdf(w3, initial_mu3 , np.sqrt(initial_sigma2w3))
APS2B_CDF_w2_conditional_u = CDF_w2
idx1 = np.where(APS2B_CDF_w2_conditional_u <= 0.5)[0]
term1 = CDF_w2 + (initial_theta12*CDF_w2)*(1 - CDF_w2)*(4*CDF_simulated_us - 1)
idx2 = np.where(APS2B_CDF_w2_conditional_u > 0.5)[0]
term2 = CDF_w2 + (initial_theta12*CDF_w2)*(1 - CDF_w2)*(3 - 4*CDF_simulated_us)
APS2B_CDF_w2_conditional_u[idx1] = term1[idx1]
APS2B_CDF_w2_conditional_u[idx2] = term2[idx2]
APS2B_CDF_w3_conditional_u = CDF_w3;
idx1 = np.where(APS2B_CDF_w3_conditional_u <= 0.5)
term1 = CDF_w3 + (initial_theta13*CDF_w3)*(1 - CDF_w3)*(4*CDF_simulated_us - 1)
idx2 = np.where(APS2B_CDF_w3_conditional_u > 0.5)
term2 = CDF_w3 + (initial_theta12*CDF_w3)*(1 - CDF_w3)*(3 - 4*CDF_simulated_us)
APS2B_CDF_w3_conditional_u[idx1] = term1[idx1]
APS2B_CDF_w3_conditional_u[idx2] = term2[idx2]
initial_pw1w2 = stats.kendalltau(x=APS2B_CDF_w2_conditional_u,
y=APS2B_CDF_w3_conditional_u)[0]
theta0 = [initial_alpha, initial_beta1, initial_beta2, initial_beta3,
initial_mu2, initial_mu3, initial_sigma2u, initial_sigma2v,
initial_sigma2w2, initial_sigma2w3, initial_pw1w2,
initial_theta12, initial_theta13]
# Bounds to ensure sigma2v and sigma2u are >= 0
bounds = [(None, None) for x in range(6)] + [
(1e-5, np.inf),
(1e-5, np.inf),
] + [(None, None) for x in range(5)]
# Minimize the negative log-likelihood using numerical optimization.
MLE_results = minimize(
fun=AppLoglikelihood_vine_APS2B,
x0=theta0,
method="Nelder-Mead",
tol = 1e-6,
options={"maxiter": 2000},
args=(y.values, X.values, P.values, us),
bounds=bounds,
)
theta = MLE_results.x # Estimated parameter vector
log_likelihood = MLE_results.fun * -1 # Log-likelihood at the solution
# Estimation of standard errors
delta = 1e-6;
grad = np.zeros((len(y), len(theta)))
for i in range(len(theta)):
theta1 = copy.deepcopy(theta)
theta1[i] = theta[i] + delta
grad[:,i] = (AppLogDen_Vine_APS2B(theta1, y.values, X.values, P.values, us) - AppLogDen_Vine_APS2B(theta, y.values, X.values, P.values, us))/delta
OPG = grad.T@grad # Outer product of the gradient
sterr = np.sqrt(np.diag(np.linalg.inv(OPG)))
return theta, sterr, log_likelihood# import data
production_data = pd.read_excel('cowing.xlsx') # Inputs and outputs are in Logarithms
y = production_data['y'] # Output
X = production_data[['X1', 'X2', 'X3']]
P = np.log(production_data[['P1', 'P2', 'P3']])
APS3A_theta, APS3A_ster, APS3A_logMLE = AppEstimate_APS3A_FMLE(y=y, X=X, P=P)
APS3B_theta, APS3B_ster, APS3B_logMLE = AppEstimate_APS3B_FMLE(y=y, X=X, P=P)
vine_APS2A_theta, vine_APS2A_ster, vine_APS2A_logMLE = AppEstimate_Vine_APS2A(y=y, X=X, P=P)
vine_APS2B_theta, vine_APS2B_ster, vine_APS2B_logMLE = AppEstimate_Vine_APS2B(y=y, X=X, P=P)
# Display the results as a table
results = pd.DataFrame(
columns=["AS3A Est", "AS3A St.Err.",
"AS3B Est", "AS3B St.Err",
"Vine AS2A Est", "Vine AS2A St.Err.",
"Vine AS2B Est", "Vine AS2B St.Err"],
index=[
r"$$\alpha$$",
r"$$\alpha_{1}$$",
r"$$\alpha_{2}$$",
r"$$\alpha_{3}$$",
r"$$\mu_{1}$$",
r"$$\mu_{2}$$",
r"$$\sigma_{u}^{2}$$",
r"$$\sigma^{2}_{v}$$",
r"$$\Sigma^{2}_{1}$$",
r"$$\Sigma^{2}_{2}$$",
r"$$\rho_{12}$$",
r"$$\theta_{12}$$",
r"$$\theta_{13}$$"
],
)
APS3A_theta = np.round(APS3A_theta.reshape(-1, 1), 3)
APS3A_ster = np.round(APS3A_ster.reshape(-1, 1), 3)
APS3B_theta = np.round(APS3B_theta.reshape(-1, 1), 3)
APS3B_ster = np.round(APS3B_ster.reshape(-1, 1), 3)
vine_APS2A_theta = np.round(vine_APS2A_theta.reshape(-1, 1), 3)
vine_APS2A_ster = np.round(vine_APS2A_ster.reshape(-1, 1), 3)
vine_APS2B_theta = np.round(vine_APS2B_theta.reshape(-1, 1), 3)
vine_APS2B_ster = np.round(vine_APS2B_ster.reshape(-1, 1), 3)
APS_frontier = np.concatenate(
[
APS3A_theta[:4], APS3A_ster[:4],
APS3B_theta[:4], APS3B_ster[:4],
vine_APS2A_theta[:4], vine_APS2A_ster[:4],
vine_APS2B_theta[:4], vine_APS2B_ster[:4],
],
axis=1,
)
APS_sigmas = np.concatenate(
[
APS3A_theta[6:10], APS3A_ster[6:10],
APS3B_theta[6:10], APS3B_ster[6:10],
vine_APS2A_theta[6:10], vine_APS2A_ster[6:10],
vine_APS2B_theta[6:10], vine_APS2B_ster[6:10],
],
axis=1,
)
APS_mu = np.concatenate(
[
APS3A_theta[4:6], APS3A_ster[4:6],
APS3B_theta[4:6], APS3B_ster[4:6],
vine_APS2A_theta[4:6], vine_APS2A_ster[4:6],
vine_APS2B_theta[4:6], vine_APS2B_ster[4:6],
],
axis=1,
)
APS_thetas = np.concatenate(
[
APS3A_theta[-3:], APS3A_ster[-3:],
APS3B_theta[-3:], APS3B_ster[-3:],
vine_APS2A_theta[-3:], vine_APS2A_ster[-3:],
vine_APS2B_theta[-3:], vine_APS2B_ster[-3:],
],
axis=1,
)
results.iloc[0:4, :] = APS_frontier
results.iloc[4:6, :] = APS_mu
results.iloc[6:10, :] = APS_sigmas
results.iloc[-3:, :] = APS_thetas
display(results)
print('APS3A LL: ', APS3A_logMLE)
print('APS3B LL: ', APS3B_logMLE)
print('Vine APS2A LL: ', vine_APS2A_logMLE)
print('Vine APS2B LL: ', vine_APS2B_logMLE)/var/folders/q0/9kb46g7n1_57dfk7vtdsv8t4w169ch/T/ipykernel_8109/1741302720.py:70: RuntimeWarning: invalid value encountered in log
logDen = np.log(r) + np.log(DenAll)| AS3A Est | AS3A St.Err. | AS3B Est | AS3B St.Err | Vine AS2A Est | Vine AS2A St.Err. | Vine AS2B Est | Vine AS2B St.Err | |
|---|---|---|---|---|---|---|---|---|
| $$\alpha$$ | -11.471 | 0.241 | -11.381 | 0.236 | -11.502 | 0.268 | -11.453 | 0.262 |
| $$\alpha_{1}$$ | 0.045 | 0.025 | 0.041 | 0.024 | 0.045 | 0.026 | 0.058 | 0.022 |
| $$\alpha_{2}$$ | 1.073 | 0.025 | 1.076 | 0.025 | 1.079 | 0.026 | 1.059 | 0.022 |
| $$\alpha_{3}$$ | 0.03 | 0.029 | 0.025 | 0.029 | 0.026 | 0.03 | 0.031 | 0.029 |
| $$\mu_{1}$$ | 1.951 | 0.591 | 2.037 | 0.64 | 1.96 | 0.61 | 1.668 | 0.415 |
| $$\mu_{2}$$ | 0.662 | 1.17 | 0.588 | 1.374 | 0.508 | 1.327 | 0.444 | 0.985 |
| $$\sigma_{u}^{2}$$ | 0.01 | 0.003 | 0.01 | 0.003 | 0.01 | 0.004 | 0.015 | 0.003 |
| $$\sigma^{2}_{v}$$ | 0.004 | 0.001 | 0.003 | 0.001 | 0.003 | 0.001 | 0.002 | 0.0 |
| $$\Sigma^{2}_{1}$$ | 0.333 | 0.032 | 0.337 | 0.034 | 0.343 | 0.035 | 0.349 | 0.036 |
| $$\Sigma^{2}_{2}$$ | 0.582 | 0.094 | 0.604 | 0.103 | 0.593 | 0.099 | 0.575 | 0.093 |
| $$\rho_{12}$$ | 0.508 | 0.1 | 0.533 | 0.097 | 0.483 | 0.101 | 0.412 | 0.107 |
| $$\theta_{12}$$ | 0.644 | 0.368 | 0.639 | 0.458 | 0.206 | 0.415 | 0.106 | 0.453 |
| $$\theta_{13}$$ | -0.17 | 0.329 | -0.089 | 0.459 | -0.22 | 0.349 | -0.118 | 0.411 |
APS3A LL: -72.52373198800693
APS3B LL: -73.12293492860093
Vine APS2A LL: -74.4857292736222
Vine APS2B LL: -77.29226482218182# Remove all previous function and variable definitions before the next exercise
%reset